Biomechanik der Koxarthrose
Die Arthrose des Hüftgelenks ist eine Krankheit mit multifaktorieller Patho-genese und schwerwiegenden Konsequenzen für Betroffene sowie sozioökonomischen Auswirkungen. Als ein wesentlicher Faktor bei der Entstehung der Koxarthrose wird die mechanische Belastung des Gelenks angesehen. In dieser Übersicht wird die aktuelle Literatur zur Bestimmung der Biomechanik des Hüftgelenks mit numerischen Methoden dargestellt. Außerdem soll der Erkenntnisgewinn aus den numerischen Berechnungen für die Ursachenforschung der Koxarthrose dargestellt werden.
Im Zeitraum 2011 bis 2014 veröffentlichte Quellen zu unterschiedlichen Simulationsmethoden wurden über PubMed identifiziert. Die Recherche-ergebnisse wurden in die Kategorien komplementäre Modelle, Mehrkörpersimulation und Finite-Elemente-Analyse aufgeteilt. Für diese Kategorien wurden typische Software-Lösungen und aktuelle Forschungsergebnisse zusammengestellt.
Die numerische Simulation der Belastung des Hüftgelenks ist ein wich-tiges Werkzeug, das zusammen mit der epidemiologischen Forschung einen wesentlichen Beitrag zur Erforschung der Entstehung der Koxarthrose beiträgt. Zusätzlich ermöglicht die biomechanische Simulation die Generierung von fundierten Empfehlungen zu Prävention und Rehabilitation.
Schlüsselwörter: Hüftgelenk – Arthrose – Mehrkörpersimulation – Finite-Elemente-Analyse
Biomechanics of hip osteoarthritis
Osteoarthritis of the hip is a disease with a multifactorial pathogenesis and severe consequences for patients. It also represents a great socio-economic burden. Mechanical loads on the joint are considered to be a key factor in the development of hip osteoarthritis. This overview presents current literature on the simulation of hip biomechanics with numerical methods. The findings from these numerical simulation studies and the part they play in research into the causes of hip osteoarthritis are also presented.
Literature sources (published 2011 to 2014) relating to different simulation methods (multibody simulation, finite element analysis and other models) were identified by using PubMed. Typical software solutions and current research findings are outlined for the individual methods.
The numerical simulation of the loads on the hip joint is an important tool that, together with epidemiological research, contributes to the under-standing of the development of hip osteoarthritis. In addition to this, biomechanical simulation makes it possible to produce informed recommendations for prevention and rehabilitation.
Keywords: hip joint – osteoarthritis – multibody simulation – finite element analysis
ASU Arbeitsmed Sozialmed Umweltmed 2015; 50: 886–895
Einführung
Die Krankheit Koxarthrose (KA) kann für Betroffene schwere Auswirkungen auf ihr Alltags- und Arbeitsleben haben (Bolen et al. 2010). Die KA ist für Erwachsene einer der häufigsten Gründe für Behinderungen (Chu et al. 2014; Ma et al. 2014) und hat eine Prävalenz von 10,9 % (systematisches internationales Review von Pereira et al. 2011). Die Krankheit verursacht eine hohe Anzahl an Arbeitsunfähigkeitstagen und hohe indirekte Kosten durch frühzeitige Berufsausstiege (Kotlarz et al. 2010; Piscitelli et al. 2012; Rabenberg 2013). Die Ursachen der Koxarthrose sind vielfältig und noch nicht vollständig erforscht. Metabolische oder genetische Faktoren können die Pathogenese beeinflussen, aber es stehen insbesondere auch mechanische Belastungen als Ursachen zur Diskussion (Felson 2004). Die Erforschung dieser mechanischen Faktoren steht in diesem Artikel im Vordergrund. Dabei haben auch Varianten der knöchernen Geometrien (z. B. Hüftdysplasie [HD] oder femoroazetabuläres Impingement [FAI]) eine große Bedeutung (Leunig et al. 2005), da sie die mechanischen Verhältnisse an der Hüfte nachhaltig beeinflussen können.
Um einen besseren Einblick in die mechanischen Ursachen der Koxarthrose zu erhalten, müssen die im Hüftgelenk wirkenden Kräfte sowie der Einfluss der Hüftgelenksmuskulatur verstanden werden. Die numerische Simulation bietet die Möglichkeit, genau diese inneren Kräfte – also Gelenk- und Muskelkräfte – zu berechnen. Für das Verständnis und die Validierung der Reaktionskräfte im Gelenk sind auch In-vivo-Daten der Hüftgelenksbelastung von großer Bedeutung. Diese werden z. B. durch Messungen mit instrumentierten Totalendoprothesen gewonnen (Bergmann 2008). Muskelkräfte können dabei aber nicht gemessen werden, ihre Bestimmung bleibt Aufgabe der Simulation. Die Datensätze der In-vivo-Messun-gen stammen außerdem vorrangig von älteren Patienten mit Hüft-gelenksersatz nach KA, weshalb Bewegungssituationen mit hohen physischen Belastungen nicht dargestellt werden können. Es ist daher eine Aufgabe der biomechanischen Simulation, die Belastungen für Aktivitäten zu berechnen, die von Gesunden durchgeführt werden können. Es sind insbesondere solche Aktivitäten interessant, die möglicherweise in einem Zusammenhang mit der Entstehung der KA stehen könnten. Dabei handelt es sich zumeist um Bewegungen, die eine hohe Belastung im Hüftgelenk hervorrufen können wie z. B. die Handhabung schwerer Lasten. In der Literatur finden sich nur Hinweise mit geringer Evidenz darauf, dass z. B. schweres Heben, aber auch sehr langes Stehen schädlich für die Hüftgelenksgesundheit sein könnten (Sulsky et al. 2012; Spahn et al. 2014). Das fehlende Verständnis für die kausalen Zusammenhänge zwischen risikoassoziierten Tätigkeiten und der Entstehung der KA unterstreicht die wichtige Funktion der numerischen Simulation als biomechanische Methode zur Überprüfung epidemiologischer Erkenntnisse. Zugleich lassen sich aber auch präventive Empfehlungen z. B. bezüglich Lastenhandhabung – auch für den Alltag – und Arbeitsplatzgestaltung aus den Ergebnissen ableiten. Die geometrischen Varianten des Hüftgelenks stellen ein weiteres Forschungsgebiet für die Simulation dar. In silico können z. B. Hüftgelenke mit HD- oder FAI-Geometrien in Hinblick auf die Belastung von Knorpel, Labrum oder Kollision untersucht werden. Die damit möglichen Schlussfolgerungen lassen unter Umständen auch eine Früherkennung von pathogenetischen Faktoren der KA z. B. im Röntgenbild zu.
Die aktuelle Literatur zur biomechanischen Simulation des Hüft-gelenks vor dem Hintergrund unterschiedlicher Belastungssituatio-nen lässt sich in drei Kategorien einteilen, die aufeinander aufbauen. Die erste Kategorie enthält Simulationen oder Berechnungen, die häufig direkt auf Bewegungsmessungen basieren, z. B. mittels Stereo-photogrammetrie und Kraftmesssensoren. Diese komplementären Modelle werden mit unterschiedlichsten Methoden erstellt und beinhalten häufig auch analytische Berechnungen. Die zweite Kategorie bildet die Mehrkörpersimulation (MKS), die häufig auf den Daten der Bewegungsmessung basiert. In die dritte Kategorie fallen Finite Elemente Analysen (FEA), welche wiederum häufig die mit der MKS berechneten Ergebnisse als Randbedingungen verwenden. Alle drei Methoden haben ihre Berechtigung, da sie entweder unterstützend fungieren oder für eine bestimmte Anwendung oder Fragestellung ein Alleinstellungsmerkmal haben.
In dieser Literaturübersicht werden Quellen vorgestellt, die seit 2011 zum Thema Simulation des Hüftgelenks und Koxarthrose publiziert wurden. Dazu wurde PubMed ( www.pubmed.gov ) durchsucht nach Kombinationen der Schlüsselworte: „hip“, „osteoarthr*“, „comput*“, „model“, „simulation“. Die Auswahl wurde nach Durch-sicht der Titel und Abstracts vorgenommen. Ausgeschlossen wurden Publikationen mit Bezug zur endoprothetischen Versorgung. Es wurden auch Artikel ohne direkten Bezug zu KA in die Literaturübersicht einbezogen, sofern sie interessante Informationen zur Biomechanik des Hüftgelenks enthalten. Ein Literatur-Review von Stops et al. (2012) behandelt die Simulation des Hüftgelenks vor 2011. Die ausgewählten Ergebnisse der Literaturrecherche wurden in die drei genannten Kategorien unterteilt und im Text nach einer Einführung in die entsprechende Kategorie mit der verwendeten Software und den erzielten Ergebnissen vorgestellt. Die Tabellen 1–3 geben einen Überblick über die Rechercheergebnisse. Es soll damit ein Einblick in die aktuellen Forschungsfragen und angewandten Methoden gewährt werden.
Komplementäre Modelle
Bei dieser Modellkategorie handelt es sich z. B. um Modelle, die in den Programmen integriert sind, die zur Aufzeichnung der Motion-Capture-Daten und der Bodenreaktionskräfte verwendet werden. Sie fallen im Vergleich zu eigenständigen MKS- oder FEA-Modellen eher einfach aus, ermöglichen es aber, mit geringem Aufwand zusätzlich zur Messung der äußeren Belastung eine Analyse der inneren Belastungen durchzuführen.
Bei den in den Aufnahmeprogrammen integrierten Modellen sind die Möglichkeiten zur Modifikation zumeist stark beschränkt, außer-dem stellen sich die Berechnungsvorgänge teilweise auch als Black Box dar. Modelle aus der Aufzeichnungssoftware werden praktisch sofort mit jeder Messung erstellt und konkurrieren somit mit der MKS, die die gleichen Daten als Eingangsgrößen verwendet. Bei händisch programmierten, teilweise analytischen, meist zweidimensionalen Modellen werden hingegen die mechanischen und anatomischen Kenntnisse der Entwickler weit mehr gefordert. Da-raus entstehen häufig anwendungsorientierte Modelle, die für ihren klar begrenzten Einsatzzweck sehr gute Ergebnisse produzieren können.
Software
Markerbasierte Aufnahmesoftwares, die auch biomechanische Berechnungen inkludieren, sind z. B. Vicon Nexus (Vicon Motion System Ltd., Oxford, GB) und VISUAL3D (Qualisys AB, Gothenburg, SE). Gleichzeitig gibt es Programme, die auf markerfreiem Motion Capture (z. B. BioStage, Organic Motion, New York, US-NY), Goniometern (z. B. Biometrics, Newport, GB) oder Akzelerometern, Magnetometern und Gyroskopen (z. B. Xsens MVN BIOMECH, Xsens Technologies B.V., Enschede, NL) basieren. Speziell programmierte Modelle werden z. B. mit Vicon BodyBuilder (Vicon Motion System Ltd., Oxford, GB), Matlab und Simulink (beide The MathWorks Inc., Natick, US-MA) o. Ä. erstellt.
Übersicht über komplementäre Modelle
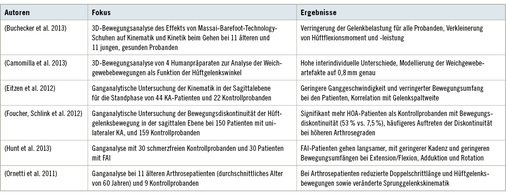
Viele der komplementären Modelle, die in der Aufnahmesoftware für Bewegungsanalysen integriert sind, werden für klinische Frage-stellungen verwendet. Da sie häufig keine größeren Modifikationen erlauben, bieten sie eine standardisierte und schnelle Auswertungsmöglichkeit. Ein Forschungsschwerpunkt ist die Analyse von Bewegungsmustern. Dazu postulierten Laroche et al. (2011), dass mit der 3D-Motion-Capture-Technik und Ganganalyse eine ausreichende Test-Retest-Reliabilität bestünde, so dass es sich dabei um adäquate Mittel zur Analyse des Gangbildes bei KA handele. Ornetti et al. (2011) haben mittels Ganganalyse die dreidimensionale Kinematik vom Gehen in der Ebene bei Patienten (n = 11) mit unilateraler KA mit der von Kontrollprobanden (n = 9) verglichen. Dabei wurde eine reduzierte Schrittlänge, reduzierte maximale Flexion und Extension für die ipsilaterale Hüfte der KA-Patienten festgestellt. Für das kontralaterale Hüftgelenk zeigte sich ebenfalls ein eingeschränkter Bewegungsumfang. Ähnliche Beobachtungen wurden auch von Eitzen et al. (2012) gemacht. Zusätzlich zeigte sich teilweise ein Zusammenhang zwischen den Ausprägungen der Bewegungsparameter und der Gelenkspaltweite. Auch Foucher et al. (2012) fanden in einer kontrollierten Studie unter Verwendung der Ganganalyse Bewegungseinschränkungen für Patienten mit KA. Dabei wurde besonders auf ein Bewegungsmuster (eine Bewegungsdiskontinuität) geachtet, das bei den KA-Patienten (n = 150) mit zunehmendem Kellgren-Lawrence-Score häufiger und bei den Kontrollen (n = 159) seltener auftritt. Die Bewegungsdiskontinuität zeigte sich während der Standphase beim Gehen in der Sagittalebene des Hüftgelenks: Dort war für schwerere Arthrosegrade kaum eine Hüftgelenksexten-sion möglich, wie sie bei Gesunden ab der mittleren Standphase auftritt. Veränderte Bewegungsmuster werden z. B. auf eine geschwächte Muskulatur (M. gluteus medius) zurückgeführt (Dwyer et al. 2013), was auch Schwierigkeiten beim Halten des Gleichgewichts (Truszczyska et al. 2014) erklären kann. Auch bei FAI-Patienten (n = 30) zeigte sich bei einer Ganganalyse im Vergleich zu Kontrollprobanden (n = 30) eine eingeschränkte Bewegungsfreiheit für Hüftgelenksextension, -adduktion und interne Rotation (Hunt et al. 2013). Weitere Informationen zu den Weg-Zeit-Parametern bei KA lieferte eine Metaanalyse von Constantinou et al. (2014).
Eine Untersuchung von Buchecker et al. (2013) beschäftige sich mit Auswirkung des Schuhwerks (Massai-Barfuß-Technologie-Schuhe (MBT) vs. Sportschuhe) auf die Belastung in den Gelenken der unteren Extremität, was Ansätze für die Prävention von KA liefern sollte. Dafür wurden 11 junge und 11 ältere, männliche Proban-den ganganalytisch untersucht und für alle Probanden wurde mit den MBT-Schuhen eine Verringerung der Hüftgelenksbelastung festgestellt.
Mehrkörpersimulation
Bei der MKS handelt es sich um die numerische Methode zur Berechnung von Mehrkörpersystemen. Dabei wird klassischerweise das Zusammenspiel von Starrkörpern und deren Gelenkverbindun-gen unter Berücksichtigung der kinetischen oder kinematischen Randbedingungen simuliert. Wichtig ist für dynamische Bewegungs-abläufe, dass die Trägheiten der Körper bei der Berechnung berücksichtigt werden. Die entstehenden Differenzialgleichungen werden z. B. nach dem Newton-Raphson-Verfahren gelöst. Bei der MKS handelt es sich um eine etablierte Methode, bei der für detaillierte Erklärungen auf eine Vielzahl an Quellen verwiesen werden kann (z. B. Kane 1985; Stelzner 2009). Eine große Herausforderung für die MKS ist die inversdynamische Simulation der Muskulatur. Da für die Ausführung einer bestimmten Gelenkbewegung mehrere Muskeln zur Verfügung stehen (Muskelredundanz) müssen Kriterien formuliert werden, nach denen die Muskelrekrutierung abläuft. Hierfür werden Optimierungsalgorithmen verwendet, die eine Verteilung der für eine bestimmte Bewegung benötigten Kraft auf die einzelnen Muskeln bewirken (Andersen 2009; Forster 2004). MKS-Modelle sind im Normalfall detaillierter gestaltet und bieten mehr Anpassungsmöglichkeiten als die komplementären Modelle, häufig ist ihre Konfiguration offen für den Anwender einsichtig und somit gut nachvollziehbar und teilweise modifizierbar.
Software
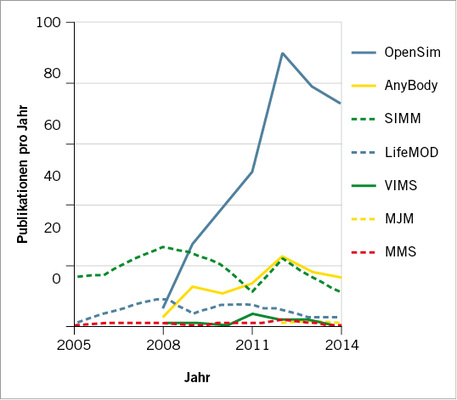
Software für die humane Mehrkörpersimulation funktioniert in den meisten Fälle nach dem Prinzip der inversen Dynamik und ermöglicht die Berechnung von Muskel- und Gelenkkräften. Als geometrische Eingangsdaten für die Modelle dienen Knochengeometrien und Ursprungs- und Ansatzpunkte der Muskulatur. Diese Geo-metrien stammen entweder aus Bilddatensätzen (CT- oder MRT-Datensätze) oder aus der Vermessung von Humanpräparaten. Die mittels Motion Capture gemessene Kinematik und z. B. über Kraftmessplatten aufgenommenen Bodenreaktionskräfte dienen als Randbedingungen für die Mehrkörpersimulation. Zu den verwendeten Programmen gehören z. B. AnyBody (AnyBody Technology A/S, Aalborg, DK, Damsgaard et al. 2006), LifeMOD (LifeModeler, Inc., San Clemente, US-CA), eine Erweiterung für die Mehrkörpersimulationssoftware MSC ADAMS (MSC Software, Newport Beach, US-CA) die 2012 von Smith & Nephew, Inc. (London, GB) akquiriert wurde, Musculoskeletal Joint Modeller (MJM, Esat 2009; Ozada 2010), OpenSim (Delp et al. 2007), Musculoskeletal Modelling in Simulink (MMS, Davoodi 2002), Software for Interactive Musculo-skeletal Modelling (SIMM, Delp 1995) und Virtual Interactive Musculoskeletal System (VIMS, Chao et al., 2007). Abbildung 1 zeigt, wie häufig die oben genannten Schlüsselpublikationen der einzelnen MKS-Software-Lösungen seit 2005 zitiert wurden und gibt dadurch einen ungefähren Eindruck der Nutzungshäufigkeit der Programme. Die Zitationshäufigkeit wurde mit einem Web-of-Science-Citation-Report ermittelt. Da es für die proprietäre Software LifeMOD keine Schlüsselpublikation gibt, wurde in diesem Fall nach „TOPIC: (life-mod)“ gesucht.
Übersicht über MKS-Modelle
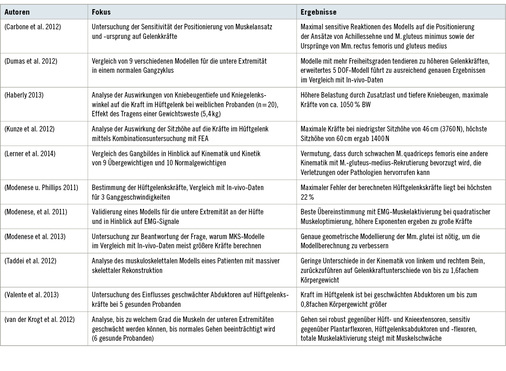
Bei der MKS sind im betrachteten Zeitraum keine KA-spezifischen Modelle zu finden, jedoch sind die Publikationen, die das Hüftgelenk untersuchen, dennoch von großer Relevanz für das Verständnis der Biomechanik des Hüftgelenks. Interessant sind z. B. die Lastverteilungen bei unterschiedlichen Anthropometrien und die Auswirkung von Muskelparametern auf Gelenkkräfte und -funktion. Lerner et al. (2014) haben das Gangbild von Übergewichtigen (n = 9) und Normalgewichtigen (n = 10) kinematisch und kinetisch miteinander verglichen. Dabei beobachteten sie, dass Übergewichtige eine Schwäche der Kniestrecker und Hüftabduktoren (M. gluteus medius) aufwiesen, was sie beim Gehen anfälliger gegenüber Verletzungen machen würde. Van der Krogt et al. (2012) untersuchten an Modellen von 6 gesunden Probanden, in welchem Umfang die Muskulatur geschwächt werden kann, bis kein normales Gehen mehr möglich ist. Die geringste Sensitivität hat der menschliche Gang dieser Studie nach gegenüber den Hüft- und Knieextensoren, die höchste gegenüber den Hüftgelenksabduktoren, -flexoren und den Plantarflexoren. Eine starke Beeinträchtigung des Gangbildes zeigte sich z. B. bei dem Modell eines Probanden ab einer Schwächung des M. gluteus medius um 60 %. Die große Abhängigkeit von den Hüftgelenksabduktoren zeigte sich auch in einer Untersuchung von Carbone et al. (2012), bei der parametrisch die Sensitivität der Positionierung von Muskelursprüngen und -ansätzen auf die Gelenk-kräfte untersucht wurde. Auch hier wurde die maximale Sensitivität für die Mm. gluteus minimus und medius ermittelt. Weitere Faktoren mit hohem Einfluss waren die Positionierung der Achillessehne und des M. rectus femoris. Valente et al. (2013) untersuchten auch vor dem Hintergrund eines möglichen Zusammenhangs zwischen geschwächten Hüftgelenksabduktoren und der KA die Auswirkung einer Schwächung derselben auf die Kräfte im Hüftgelenk an 5 gesunden Probanden. Dabei wurde eine Vergrößerung der Gelenkkraft um das 0,2–0,8fache Körpergewicht beobachtet. Modenese et al. (2013) analysierten die Muskelmodellierung vor dem Hintergrund, dass mit MKS häufig Gelenkkräfte berechnet werden, die im Vergleich zu In-vivo-Daten größer sind. Dabei fanden sie, dass insbesondere die geometrische Modellierung der Mm. glutei eine große Auswirkung auf die Simulationsergebnisse hat und deshalb besonders exakt durchgeführt werden muss.
Gelenkdefinitionen sind eine weitere Schwierigkeit bei der Modellierung von MKS. Dumas et al. (2012) fanden für neun verschie-dene Modelle mit 5 (sphärisches Hüftgelenk, Scharniergelenk in Knie und Sprunggelenk) bis 9 (überall sphärische Gelenke) Freiheitsgraden (FHG) für die untere Extremität, dass bei mehr Zwangsbedingungen größere Gelenkreaktionskräfte berechnet werden. 5-FHG-Modelle zeigten aber ausreichend gute Übereinstimmung mit In-vivo-Daten. Bei MKS-Modellen kann es zu Ungenauigkeiten aufgrund von Weichteilartefakten kommen, da die Marker für das Motion Mapping im Normalfall auf der Haut aufgebracht werden. Um diese Ungenauigkeiten zu verringern, wurden Modelle vorgeschlagen, die den Fehler verringern sollen (Bonci et al. 2014; Camo-milla et al. 2013).
Kunze et al. (2012) untersuchten die Belastung im Hüftgelenk beim Hinsetzen auf einen Stuhl für unterschiedliche Sitzhöhen. Dabei lag die berechnete maximale resultierende Hüftgelenksreaktionskraft bei 3760 N, bei der niedrigsten Sitzhöhe von 46 cm. Bei einer größeren Sitzhöhe von 60 cm lag die Belastung im Hüftgelenk nur noch bei 1400 N. Haberly (2013) berechnete bei Kniebeugen mit weiblichen Probandinnen (n = 20) mit zusätzlicher Gewichtsweste (5,4 kg) maximale Hüftgelenksreaktionskräfte vom 10,5fachen Körpergewicht, ein Wert, der vor den bekannten Größenordnungen als wenig realistisch einzuschätzen ist. Bei allen Studien ist die Abhän-gigkeit der Hüftgelenksreaktionskraft von der Kniebeugentiefe zu erkennen, was auf die Hebelarme der Hüftgelenksmuskulatur zurückzuführen ist (Németh et al. 1985). Für den Gang in der Ebene hingegen ergeben sich unterschiedliche Belastungen des Hüftgelenks in Abhängigkeit von der Ganggeschwindigkeit. Modenese u. Phillips (2011) verglichen dafür in vivo gemessene und simulierte Hüftgelenksreaktionskräfte für drei Patienten und drei Geschwindig-keiten. Der maximale relative Fehler gegenüber den Messungen betrug mit dem verwendeten Modell 22 %. Welche Auswirkungen geringe Unterschiede im Gangbild haben können, zeigten Taddei et al. (2012) in einer Fallstudie, bei der bei einem Patienten mit massiver Rekonstruktion eines Femurs das Gangbild untersucht wurde. Dabei fanden sich im Hüftgelenk der operierten Seite Kräfte, die bis zum 1,6fachen des Körpergewichts größer waren als auf der gesunden Seite.
Finite-Elemente-Analyse
Die Finite-Elemente-Methode ist ebenfalls eine numerische Methode zur Lösung von Differenzialgleichungen. Dabei wird ein großes mechanisches Problem in eine finite Zahl von kleineren diskretisiert und so gelöst. Weitere Informationen zu diesem Verfahren finden sich z. B. bei Bathe (2002). Wie auch die MKS benötigt die FEA Geometrien und Randbedingungen. Die Geometrien stammen auch hier typischerweise aus bildgebenden Verfahren. Die Ergebnisse aus den makroskopischen MKS-Berechnungen können verwendet werden, um mit der FEA mikroskopische Analysen durchzuführen. Alternativen für Randbedingungen sind Daten aus In-vivo-Messungen (z. B. Bergmann 2008) oder klassischen 2D-Modellen (Pauwels 1973; Debrunner 1975). Typisch ist ein Übertragen von Gelenk- und Muskelkräften auf ein FEA-Modell, um die Auswirkung auf Knochen- und Knorpelstrukturen zu untersuchen. Die FEA bietet die Möglichkeit mit Materialeigenschaften zu arbeiten, so dass Verformungen und Spannungen von Körpern berechnet werden können. Diese Eigenschaften werden häufig aus mechanischen Versuchen mit biologischem Gewebe ermittelt.
Software
Typische, bei der FEA angewendete, proprietäre Software-Pakete sind z. B. Abaqus (Dassault Systèmes S.A., Vélizy-Villacoublay, FR), ANSYS (ANSYS Inc., Canonsburg, US-PA) oder Nastran (MSC Soft-ware, Newport Beach, US-CA. Eine freie Alternative ist z. B. FEBIO (febio.org, University of Utah und Columbia University), die mit den kommerziellen Lösungen vergleichbare Ergebnisse erreichen soll (Maas et al. 2009). Da die FEA-Simulationen besonders rechenintensiv sind, ist die verwendete Hardware wichtig. Die Programme unterscheiden sich in der Recheneffizienz und in der Unterstützung von Grafikprozessoren.
Übersicht über FEA-Modelle
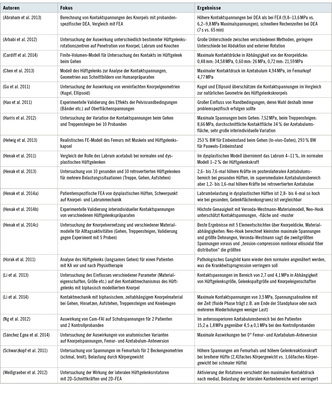
Die FEA erlaubt es, Informationen über die Zustände im Hüftgelenk bei unterschiedlichen Geometrien und für unterschiedliche Last-situationen zu gewinnen. Aus der Analyse der Knorpelverformungen lassen sich z. B. mögliche Zusammenhänge zwischen den geometrischen Verhältnissen (HD, FAI) und der lokalen mechanischen Belastung des Gelenkknorpels ziehen. So haben Henak et al. (2011) verglichen, ob das Labrum acetabuli eine unterschiedliche Rolle bei gesunden und dysplastischen Hüftgelenken spielt und dazu jeweils eine Geometrie untersucht. Für die dysplastische Hüfte übernahm das Labrum einen wesentlich größeren Anteil der Belastung als bei der gesunden (4–11 % vs. 1–2 %). Für alle simulierten Bewegungen (Gehen und Treppensteigen) übernahm das Labrum beim dysplastischen Hüftgelenk mehr als die doppelte Last im Vergleich zum gesunden Gelenk. Die maximalen Kontakt-spannungen lagen im Bereich von 6–14 MPa. Nachdem eine größere Anzahl von dysplastischen (n = 10) und gesunden (n = 10) Hüftgelenken untersucht wurde, zeigte sich, dass das Labrum der dysplastischen Hüften ein 4faches der Last im Vergleich zum Labrum eines gesunden Hüftgelenks trägt (Henak et al. 2014a). Bei den Knorpelbelastungen und der Gelenkkongruenz wurden hingegen keine Unterschiede festgestellt. Eine weitere Studie der gleichen Arbeitsgruppe widmete sich der Frage der Auswirkung von retrovertierten Azetabulae (jeweils 10 Hüftgelenke mit retrovertiertem Azetabulum und 10 gesunde Hüftgelenke) beim Gehen, Treppensteigen, Hinsetzen und Aufstehen (Henak et al. 2013). Dabei fan-den sich im posteorolateralen Azetabulumsbereich bei den gesunden Hüften 2,6- bis 7,6-mal größere Kontaktspannungen. Im superomedialen Bereich waren die Kräfte bei den retrovertierten Azetabulae dafür 1,2- bis 1,6-mal höher. Die maximalen Kontakt-spannungen lagen hier im Bereich von ca. 5–15 MPa. Auch Sán-chez Egea et al. (2014) widmeten sich der Fragestellung der Auswirkung von retrovertierten Azetabulae, aber auch von retrovertierten Femora. Dabei fanden sie im Vergleich zu gesunden Geometrien höhere hydrostatische Drücke. Für die gesunden Geometrien lagen die Drücke vorrangig im Bereich von 2–3,5 MPa, während die retrovertierten Geometrien Drücke von bis zu 5 MPa erreichten. Mit Modellen für zwei Cam-FAI-Patienten und zwei zugehörigen Kontrollprobanden haben Ng et al. (2012) versucht, den möglichen Zusammenhang zwischen KA und der FAI zu erklären: Für die pathologischen Geometrien ergaben sich dabei maximale Schubspannungen von 15,2 ± 1,8 MPa, für die gesunden 4,5 ± 0,1 MPa. In einer Fallstudie haben Horak et al. (2011) für einen Patienten mit KA (Kellgren-Lawrence-Score 1) untersucht, wie sich eine physiotherapeutische Behandlung über 8 Monate auf die Belastungssituation im Hüftgelenk auswirkt. Dabei wurde eine Abnahme des Kontaktdrucks von 7,5 auf 3,5 MPa beim Gehen berechnet.
Auch die Simulation gesunder Hüftgelenke ist für die Arthroseforschung von großer Bedeutung, da Vergleichswerte nötig sind, um die Ergebnisse der pathologischen Gelenke interpretieren zu können. Das gesunde Hüftgelenk wurde von Harris et al. (2012) beim Gehen und Treppensteigen analysiert. Beim Gehen fanden sich die größten Kräfte beim Aufsetzen der Ferse: maximale Kontaktspannungen von 7,5 ± 2,1 MPa bei einer Belastung vom 2,3fachen Körpergewicht. Beim Treppensteigen ergab sich die maximale Be-lastung für den Fersenauftritt beim Herabsteigen: 8,7 ± 3 MPa und 2,6faches Körpergewicht. Bei beiden Aktivitäten fand sich eine durchschnittliche Kontaktfläche von 35 % des Azetabulumknorpels. Im Modell von Chen et al. (2013), das einfache linear elastische Materialen für den Knorpel verwendet, wurde ein maximaler Druck von 4,9 MPa bestimmt. Li et al. (2014) simulierten für neun alltägliche Aktivitäten (langsames, normales und schnelles Gehen, Hinsetzen, Aufstehen, Treppenauf- und absteigen, Kniebeuge) die Knorpelspan-nungen. Die höchsten maximalen Spannungen für die einzelnen Aktivitäten wurden beim Treppenabsteigen (3,5 MPa) und die geringsten beim Kniebeugen (1,8 MPa) berechnet. Unter Verwen-dung der Finite-Volumen-Methode haben Cardiff et al. (2014) die Spannungen für verschiedene Knorpeldicken ausgewertet. Bei der geringsten modellierten Knorpeldicke von 0,48 mm ergaben sich maximale Spannungen von 34,6 MPa, bei der größten modellierten Dicke waren es dagegen 21,6 MPa. Abraham et al. (2013) verglichen zur Berechnung der Kontaktspannungen beim Gehen und Treppensteigen im Hüftgelenk die FEA mit der Diskrete-Elemente-Methode (DEA), die wesentlich kürzere Rechenzeiten ermöglichte (in diesem Fall: DEA 7 s vs. FEA 65 min). Bei der DEA ergaben sich jedoch etwas größere maximale (9,8–13,6 MPa vs. 6,2–9,8 MPa) und durchschnittliche (3,0–3,7 MPa vs. 2,0–2,5 MPa) Kontaktspannungen. Die Kontaktmuster waren aber vergleichbar. Die größeren Kontakt-spannungen wurden auf den fehlenden Poisson-Effekt bei der DEA-Methode zurückgeführt.
Wichtig bei der Simulation des Hüftgelenks ist die Verwendung von realistischen Geometrien. Gu et al. (2011) untersuchten, welche Auswirkungen die Verwendung einer Best-fit-Kugel bzw. eines Ellipsoids hat. Dabei zeigte sich, dass die einfachen Geometrien die Spannungen überschätzten (maximale Spannung im Azetabulum: 19 MPa bei Kugel, 17 MPa bei Ellipsoid, 15 MPa bei natürlicher Geometrie). Ein gegenteiliges Ergebnis veröffentlichten Anderson et al. (2010). Dort wurde berechnet, dass die idealisierten Geometrien die Kontaktspannungen unter- und dafür die Kontaktfläche überschätzen. Beide Veröffentlichungen weisen aber darauf hin, dass mit realen Geometrien die wirklichkeitsnahsten Ergebnisse gewonnen werden können. Auch die Pelvisrandbedingungen können einen Einfluss auf das Gelenk haben, da sie die Pelvismechanik stark beeinflussen (Hao et al. 2011). Die Beckenbreite habe nach einer Studie an weib-lichen Becken von Schwarzkopf et al. (2011) auch einen entscheiden-den Einfluss auf die Kräfte im Hüftgelenk. Diese Gelenkkräfte steigen demnach proportional zum Quotienten aus Hüftgelenksbreite und Abduktorhebelarm. Auch die Stärke der lateralen Hüftgelenksrotatoren spielt eine wichtige Rolle für das Kontaktverhalten im Hüft-gelenk. Bei ihrer Aktivierung sänken die Kontaktdrücke im lateralen Bereich und verteilten sich dann mehr im medialen Bereich des Gelenks. Ein weiterer Einflussfaktor auf die Simulationsergebnisse wurde von Arbabi et al. (2012) untersucht: Die geometrische Ausrichtung von Femur und Pelvis zueinander vor dem Hintergrund des gewählten Hüftgelenksrotationszentrums. Dabei wurden je nach Methode unterschiedliche Durchdringungen festgestellt und postu-liert, dass dies große Auswirkungen auf die Simulationsergebnisse habe. Dazu ist allerdings anzumerken, dass diese Durchdringungen kein Problem darstellen müssen, da sie durchaus von der FEA-Software mitsamt dem kompletten Kontakt gelöst werden können und nur in manchen Fällen Konvergenzprobleme auftreten. Sehr wichtig für ein FEA-Modell sind natürlich auch die gewählten Material-eigenschaften. In einer kleinen Parameterstudie (Materialeigenschaften, Durchmesser von Femurkopf und Pfanne sowie Knorpeldicke) zeigten Li et al. (2013), dass durch Veränderungen an diesen Größen der maximale Kontaktstress zwischen 2,7 und 4,1 MPa schwanken kann. Henak et al. (2014b) führten eine Validierungsstudie mit Experiment zum gleichen Thema für fünf Humanpräparate durch. Die Simulationsergebnisse mit unterschiedlichen Materialmodellen (Neo-Hook und Veronda-Westman) wurden mit einem äquivalenten Experiment verglichen. Die Wahl präparatspezifischer oder für einzelne Knorpelregionen unterschiedlicher Materialeigenschaften erhöhte nicht die Ergebnisgenauigkeit hinsichtlich Kontaktspannungen oder -mustern, da gegenüber diesen Parametern nur eine geringe Sensitivität vorlag. Eine weitere Studie von Henak et al. (2014c) untersuchte erneut für verschiedene Materialmodelle, welche Elementgröße bei der Vernetzung gewählt werden sollte, um zu einem In-situ-Versuch (fünf Humanpräparate) vergleichbare Ergebnisse zu erhalten. Dabei wurde die Modellierung von 5 Elementschichten über die Knorpeldicke als beste Lösung angesehen.
Verifikation und Validierung
Für jede Simulation gilt, dass sie validiert oder verifiziert werden muss. Nur so ist es möglich, ihre Aussagekraft zu bewerten. Die dabei angewendete Methode variierte abhängig von der Frage-stellung. Da es sich bei den meisten Modellen, insbesondere den MKS- und FEA-Modellen, um sehr große und komplexe Systeme handeln kann, ist es nicht immer möglich, jeden Parameter individuell zu untersuchen. Die Priorität der Überprüfung liegt auf dem Teilsystem, das der Beantwortung der Fragestellung dient. Es ist also nicht zwingend notwendig, dass das vollständige Modell mit jedem seiner Teilsysteme dem natürlichen Vorbild entspricht. Für die MKS des Hüftgelenks sind z. B. Berechnungen in der oberen Extremität nicht relevant.
Bei der Untersuchung von Modellen wird zwischen der Verifikation und der Validierung unterschieden (Henninger et al. 2010; Lund et al. 2012). Bei der Verifikation soll die interne Plausibilität des Modells gegeben sein, das heißt z. B., dass mathematische Verfahren zuverlässig durchgeführt werden. Die Validierung befasst sich dagegen damit, ob das Modell die Fragestellung richtig abbildet und korrekt beantwortet. Eine wichtige Methode für numerische Modelle ist die Durchführung von Sensitivitätsanalysen. Dabei kann verifiziert werden, ob bestimmte Ergebnisse nur die Folge einer bestimmten Modellkonfiguration oder eines bestimmten numerischen Verhaltens sind. Die Auswahl der Parameter für diese Sensitivitätsstudien kann auf Grundlage unterschiedlicher Verfahren erfolgen. So ist es möglich, manuell oder durch stochastische Verfahren (z. B. Monte-Carlo-Simulationen, bei Valente et al. 2013) Werte vorzugeben. Ein typisches Validierungsverfahren in der Biomechanik ist der Vergleich mit Experimenten. Bei Tests mit Humanpräparaten können die Verformungen und Dehnungen der Probe mit den Ergebnissen der FEA verglichen werden. Für die Messung von Kontaktdrücken kann im Experiment z. B. eine drucksensitive Messfolie verwendet werden (z. B. Henak et al. 2014b). Wichtig sind auch die In-vivo-Messungen mit Endoprothesen, die mit Kraftaufnehmern ausgestattet sind, um berechnete Gelenkreaktionskräfte einschätzen zu können (z. B. Datenbank www.orthoload.com ). Bei der MKS wird teilweise auch mit den Ergebnissen elektromyographischer Messungen verglichen, die die Muskelaktivierung bei den Patienten aufzeichnen. Hier besteht aber die Schwierigkeit, dass das EMG-Signal nicht direkt auf die Muskelaktivierung des Modells übertragbar ist. Die Muskelaktivierung und auch die Gelenkkräfte im MKS-Modell sind außerdem sehr stark abhängig von dem gewählten Optimierungskriterium (Modenese et al. 2011), was den Vergleich weiter erschwert. Wenn experimentell eine Parameterstudie durchgeführt wird, kann es auch möglich sein, Trends in den Ergebnissen zu erkennen. Dies erlaubt die Berechnung von weiteren, nicht experimentell validierten Modellzuständen, die aber aufgrund der Vorberechnungen besser eingeschätzt werden können. Es muss für jedes Modell einzeln entschieden werden, ob die verwendeten Verifizierungs- und Validierungsverfahren ausreichende Aussagekraft haben, um das Modell als adäquat für die spezifische Fragestellung anzusehen.
Schlussfolgerung
Diese Literaturübersicht erhebt aufgrund der Beschränkung auf die Suche mit der Suchmaschine PubMed keinen Anspruch auf Vollständigkeit im Sinne eines systematischen Reviews, gibt jedoch einen guten Überblick über wesentliche Themen und Richtungen der aktuellen Forschung. Die ständig wachsende Anzahl an Publikationen zum Thema Biomechanik des Hüftgelenks und KA ermöglicht ein zunehmendes Verständnis der Krankheitsätiologie und deren Zusammenhang mit der mechanischen Belastung des Hüftgelenks. Die Simulationen zeigten z. B., dass gewisse geometrische Varianten wie Hüftdysplasie eine höhere Knorpelbelastung erzeugen als gesunde Geometrien. Wichtig ist natürlich die Untermauerung der untersuchten Risikofaktoren durch epidemiologische Evidenz. Für die Hüftdysplasie zeigte sich z. B. auch epidemiologisch, dass sie mit hoher Wahrscheinlichkeit (Odds Ratio bis zu 5,45) zur Kox-arthrose führt (Agricola et al. 2013). Jedoch sind zumindest vor dem beruflichen Hintergrund zurzeit keine eindeutigen Aussagen zu machen. Es gibt zwar bestimmte Tätigkeiten, die als risikoassoziiert bewertet werden können (z. B. schweres Heben), es besteht dazu jedoch keine endgültige Evidenz (Spahn et al. 2014; Sulsky et al. 2012). Die numerische Simulation ermöglicht es im Vergleich zu epidemiologischen Studien, sehr schnell mögliche Risikofaktoren zu identifizieren. Im Modell können z. B. mit geringerem Aufwand unterschiedliche Gelenkgeometrien oder Belastungssituationen dargestellt werden. Aus den Ergebnissen lassen sich anschließend u. a. Informationen zu den Knorpelbelastungen gewinnen, die eine Einschätzung ermöglichen, ob eine bestimmte Belastungssituation als riskant zu bewerten ist. Die so identifizierten Risikofaktoren können dann wiederum epidemiologisch untersucht wer-den. Umgekehrt kann die Simulation verwendet werden, um epidemiologisch identifizierte Risikofaktoren besser zu erklären. Da es die Simulation ermöglicht, auch hier wieder vergleichsweise flexibel Varianten der Faktoren zu überprüfen, kann sie auch Ideen zur Prävention liefern. Häufig gibt es aber keine direkte Praxisnähe bei den MKS- und FEA-Modellen, aus denen sich direkte Handlungsempfehlungen ableiten lassen, da es sich vorwiegend um Grundlagenforschung handelt. Erst durch die Kombination mit epidemiologischen Methoden zeigt sich dann die Relevanz dieser Forschungsfelder. Ein großer Nutzen für die Arbeitsmedizin zeigt sich aber bei komplementären Modellen, die in Kombination mit Messungen an Arbeitsplätzen arbeiten, und eine schnelle Rückmeldung zu Belastungen geben (z. B. das CUELA-System; Ellegast et al. 2010). Sie ermöglichen es, direkt Bewegungsausführungen aufzudecken, die sich ungünstig auf den muskuloskelettalen Apparat auswirken können, und insbesondere auch die Zeitdauern bestimmter Belastungssituationen im Arbeitsalltag zu bestimmen. Somit ist die Simulation ein wesentliches Werkzeug bei der Erforschung der Biomechanik des Hüftgelenks und der Entstehung der Koxarthrose.
Literatur
Abraham CL, Maas SA, Weiss JA, Ellis BJ, Peters CL, Anderson AE: A new dis-crete element analysis method for predicting hip joint contact stresses. J Biomech 2013; 46: 1121–1127.
Agricola R, Heijboer MP, Roze RH, Reijman M, Bierma-Zeinstra SMA, Verhaar JAN, Weinans H, Waarsing JH: Pincer deformity does not lead to osteoarthritis of the hip whereas acetabular dysplasia does: acetabular coverage and development of osteoarthritis in a nationwide prospective cohort study (CHECK). Osteoarthritis Cartilage 2013; 21: 1514–1521.
Andersen MS: Kinematically Over-determinate Musculoskeletal Systems (disserta-tion). Aalborg University, Denmark, 2009.
Anderson AE, Ellis BJ, Maas SA, Weiss JA: Effects of idealized joint geometry on finite element predictions of cartilage contact stresses in the hip. J Biomech 2010; 43: 1351–1357.
Arbabi E, Schmid J, Boulic R, Thalmann D, Magnenat-Thalmann N: Sensitivity of hip tissues contact evaluation to the methods used for estimating the hip joint center of rotation. Med Biol Eng Comput 2012; 50: 595–604.
Bathe K-J: Finite-Elemente-Methoden. 2. Aufl. Berlin: Springer, 2002.
Bergmann G (Hrsg.): OrthoLoad. www.OrthoLoad.com Zugriff: 18.12.2014
Bolen J, Schieb L, Hootman JM, Helmick CG, Theis K, Murphy LB, Langmaid G: Differences in the prevalence and severity of arthritis among racial/ethnic groups in the United States, National Health Interview Survey, 2002, 2003, and 2006. Prev Chronic Dis 2010; 7: A64.
Bonci T, Camomilla V, Dumas R, Chèze L, Cappozzo A: A soft tissue artefact model driven by proximal and distal joint kinematics. J Biomech 2014; 47: 2354–2361.
Buchecker M, Lindinger S, Pfusterschmied J, Müller E: Effects of age on lower extremity joint kinematics and kinetics during level walking with Masai barefoot technology shoes. Eur J Phys Rehabil Med 2013; 49: 675–686.
Camomilla V, Cereatti A, Chèze L, Cappozzo A: A hip joint kinematics driven model for the generation of realistic thigh soft tissue artefacts. J Biomech 2013; 46: 625–630.
Carbone V, van der Krogt MM, Koopman HFJM, Verdonschot N: Sensitivity of subject-specific models to errors in musculo-skeletal geometry. J Biomech 2012; 45: 2476–2480.
Cardiff P, Kara A, FitzPatrick D, Ivankovi A: Development of a hip joint model for finite volume simulations. J Biomech Eng 2014; 136: 011006.
Chao EYS, Armiger RS, Yoshida H, Lim J, Haraguchi N: Virtual Interactive Musculoskeletal System (VIMS) in orthopaedic research, education and clinical patient care. J Orthop Surg Res 2007; 2: 2.
Chen G-X, Yang L, Li K, He R, Yang B, Zhan Y, Wang Z-J, Yu B-N, Jian Z: A three-dimensional finite element model for biomechanical analysis of the hip. Cell Biochem Biophys 2013; 67: 803–808.
Chu CR, Millis MB, Olson SA: Osteoarthritis: From Palliation to Prevention: AOA Critical Issues. J Bone Joint Surg Am 2014; 96: e130(1)–(9).
Constantinou M, Barrett R, Brown M, Mills P: Spatial-temporal gait characteris-tics in individuals with hip osteoarthritis: a systematic literature review and meta-analysis. J Orthop Sports Phys Ther 2014; 44: 291–B7.
Damsgaard M, Rasmussen J, Christensen ST, Surma E, de Zee M: Analysis of musculoskeletal systems in the AnyBody Modeling System. Simul Model Pract Theory 2006; 14: 1100–1111.
Davoodi R, Loeb GE: A Software Tool for Faster Development of Complex Models of Musculoskeletal Systems and Sensorimotor Controllers in Simulink. J Appl Bio-mech 2002; 18: 357–365.
Debrunner HU: Studien zur Biomechanik des Hüftgelenkes I. Z Orthop Ihre Grenz-geb 1975; 113: 377–388.
Delp SL, Loan JP: A graphics-based software system to develop and analyze models of musculoskeletal structures. Comput Biol Med 1995; 25: 21–34.
Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG: OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans Biomed Eng 2007; 54: 1940–1950.
Dumas R, Moissenet F, Gasparutto X, Cheze L: Influence of joint models on lower-limb musculo-tendon forces and three-dimensional joint reaction forces during gait. Proc Inst Mech Eng Part H J Eng Med 2012; 226: 146–160.
Dwyer MK, Stafford K, Mattacola CG, Uhl TL, Giordani M: Comparison of glu-teus medius muscle activity during functional tasks in individuals with and without osteoarthritis of the hip joint. Clin Biomech 2013; 28: 757–761.
Eitzen I, Fernandes L, Nordsletten L, Risberg MA: Sagittal plane gait characteris-tics in hip osteoarthritis patients with mild to moderate symptoms compared to healthy controls: a cross-sectional study. BMC Musculoskelet Disord 2012; 13: 258.
Ellegast RP, Hermanns I, Schiefer C: Feldmesssystem CUELA zur Langzeit-erfassung und -analyse von Bewegungen an Arbeitsplätzen. Z Arbeitswiss 2010; 64: 101–110.
Esat II, Ozada N: Articular human joint modelling. Robotica 2009; 28: 321.
Felson DT: Risk Factors for Osteoarthritis. Clin Orthop Relat Res 2004; 427: S16–S21.
Forster E: Predicting Muscle Forces in the Human Lower Limb during Locomotion. Düsseldorf: VDI Verlag, 2004.
Foucher KC, Schlink BR, Shakoor N, Wimmer MA: Sagittal plane hip motion reversals during walking are associated with disease severity and poorer function in subjects with hip osteoarthritis. J Biomech 2012; 45: 1360–1365.
Gu D-Y, Hu F, Wei J-H, Dai K-R, Chen Y-Z: Contributions of non-spherical hip joint cartilage surface to hip joint contact stress. Conf Proc IEEE Eng Med Biol Soc 2011; 2011: 8166–8169.
Haberly GJ: Hip Loading During the Squat Exercise (Master’s Thesis). Oregon State University, USA, 2013.
Hao Z, Wan C, Gao X, Ji T: The effect of boundary condition on the biomechanics of a human pelvic joint under an axial compressive load: a three-dimensional finite element model. J Biomech Eng 2011; 133: 101006.
Harris MD, Anderson AE, Henak CR, Ellis BJ, Peters CL, Weiss JA: Finite element prediction of cartilage contact stresses in normal human hips. J Orthop Res 2012; 30: 1133–1139.
Helwig P, Hindenlang U, Hirschmüller A, Konstantinidis L, Südkamp N, Schnei-der R: A femoral model with all relevant muscles and hip capsule ligaments. Comput Methods Biomech Biomed Engin 2013; 16: 669–677.
Henak CR, Ellis BJ, Harris MD, Anderson AE, Peters CL, Weiss JA: Role of the acetabular labrum in load support across the hip joint. J Biomech 2011; 44: 2201–2206.
Henak CR, Carruth ED, Anderson AE, Harris MD, Ellis BJ, Peters CL, Weiss JA: Finite element predictions of cartilage contact mechanics in hips with retroverted acetabula. Osteoarthritis Cartilage 2013; 21: 1522–1529.
Henak CR, Abraham CL, Anderson AE, Maas SA, Ellis BJ, Peters CL, Weiss JA: Patient-specific analysis of cartilage and labrum mechanics in human hips with acetabular dysplasia. Osteoarthritis Cartilage 2014a; 22: 210–217.
Henak CR, Kapron AL, Anderson AE, Ellis BJ, Maas SA, Weiss JA: Specimen-specific predictions of contact stress under physiological loading in the human hip: validation and sensitivity studies. Biomech Model Mechanobiol 2014b; 13: 387–400.
Henak CR, Ateshian GA, Weiss JA: Finite element prediction of transchondral stress and strain in the human hip. J Biomech Eng 2014c; 136: 021021.
Henninger HB, Reese SP, Anderson AE, Weiss JA: Validation of computational models in biomechanics. Proc Inst Mech Eng Part H J Eng Med 2010; 224: 801–812.
Horak Z, Kubovy P, Stupka M, Horakova J: Biomechanical factors influencing the beginning and development of osteoarthritis in the hip joint. Wien Med Wochen-schr 2011; 161: 486–492.
Hunt MA, Gunether JR, Gilbart MK: Kinematic and kinetic differences during walking in patients with and without symptomatic femoroacetabular impingement. Clin Biomech 2013; 28: 519–523.
Kane TR, Levinson DA: Dynamics: Theory and Applications. New York: McGraw-Hill Book Company, 1985.
Kotlarz H, Gunnarsson CL, Fang H, Rizzo JA: Osteoarthritis and absenteeism costs: evidence from US National Survey Data. J Occup Environ Med 2010; 52: 263–268.
Kunze M, Schaller A, Steinke H, Scholz R, Voigt C: Combined multi-body and finite element investigation of the effect of the seat height on acetabular implant stability during the activity of getting up. Comput Methods Programs Biomed 2012; 105: 175–182.
Laroche D, Duval A, Morisset C, Beis J-N, D’Athis P, Maillefert J-F, Ornetti P: Test-retest reliability of 3D kinematic gait variables in hip osteoarthritis patients. Osteoarthritis Cartilage 2011; 19: 194–199.
Lerner ZF, Board WJ, Browning RC: Effects of obesity on lower extremity muscle function during walking at two speeds. Gait Posture 2014; 39: 978–984.
Leunig M, Ganz R: Femoroacetabuläres Impingement. Häufige Ursache von zur Arthrose führenden Hüftbeschwerden. Unfallchirurg 2005; 108: 9–10, 12–17.
Li J, Stewart TD, Jin Z, Wilcox RK, Fisher J: The influence of size, clearance, carti-lage properties, thickness and hemiarthroplasty on the contact mechanics of the hip joint with biphasic layers. J Biomech 2013; 46: 1641–1647.
Li J, Hua X, Jin Z, Fisher J, Wilcox RK: Biphasic investigation of contact mechanics in natural human hips during activities. Proc Inst Mech Eng Part H J Eng Med 2014; 228: 556–563.
Lund ME, de Zee M, Andersen MS, Rasmussen J: On validation of multibody musculoskeletal models. Proc Inst Mech Eng Part H J Eng Med 2012; 226: 82–94.
Ma VY, Chan L, Carruthers KJ: Incidence, prevalence, costs, and impact on dis-ability of common conditions requiring rehabilitation in the United States: stroke, spinal cord injury, traumatic brain injury, multiple sclerosis, osteoarthritis, rheumatoid arthritis, limb loss, and back pa. Arch Phys Med Rehabil 2014; 95: 986–995e1.
Maas SA, Ellis BJ, Rawlins DS, Weiss JA: A Comparison of FEBio, ABAQUS, and NIKE3D. Results for a Suite of Verification Problems. Salt Lake City: Scien-tific Computing and Imaging Insitute, University of Utah, 2009.
Modenese L, Phillips ATM: Prediction of hip contact forces and muscle activations during walking at different speeds. Multibody Syst Dyn 2011; 28: 157–168.
Modenese L, Phillips ATM, Bull AMJ: An open source lower limb model: Hip joint validation. J Biomech 2011; 44: 2185–2193.
Modenese L, Gopalakrishnan A, Phillips ATM: Application of a falsification stra-tegy to a musculoskeletal model of the lower limb and accuracy of the predicted hip contact force vector. J Biomech 2013; 46: 1193–1200.
Németh G, Ohlsén H: In vivo moment arm lengths for hip extensor muscles at dif-ferent angles of hip flexion. J Biomech 1985; 18: 129–40.
Ng KCG, Rouhi G, Lamontagne M, Beaulé PE: Finite Element Analysis Examin-ing the Effects of Cam FAI on Hip Joint Mechanical Loading Using Subject-Specific Geometries During Standing and Maximum Squat. HSS J 2012; 8: 206–212.
Ornetti P, Laroche D, Morisset C, Beis JN, Tavernier C, Maillefert J-F: Three-dimensional kinematics of the lower limbs in hip osteoarthritis during walking. J Back Musculoskelet Rehabil 2011; 24: 201–208.
Ozada N, Esat II: MJM-1 Musculoskeletal Joint Modeller (MJM) Software. J Bio-mech 2010; 43: S15–S16.
Pauwels F: Atlas zur Biomechanik der gesunden und kranken Hüfte: Prinzipien, Technik und Resultate einer kausalen Therapie. Berlin: Springer, 1973.
Pereira D, Peleteiro B, Araújo J, Branco J, Santos RA, Ramos E: The effect of osteo-arthritis definition on prevalence and incidence estimates: a systematic review. Osteoarthritis Cartilage 2011; 19: 1270–1285.
Piscitelli P, Iolascon G, Di Tanna G, Bizzi E, Chitano G, Argentiero A, Neglia C, Giolli L, Distante A, Gimigliano R, Brandi ML, Migliore A: Socioeconomic burden of total joint arthroplasty for symptomatic hip and knee osteoarthritis in the Italian population: a 5-year analysis based on hospitalization records. Arthritis Care Res 2012; 64: 1320–1327.
Rabenberg M: Gesundheitsberichterstattung des Bundes. Heft 54: Arthrose. Berlin: Robert Koch-Institut, 2013.
Sánchez Egea AJ, Valera M, Parraga Quiroga JM, Proubasta I, Noailly J, Lacroix D: Impact of hip anatomical variations on the cartilage stress: A finite element analy-sis towards the biomechanical exploration of the factors that may explain primary hip arthritis in morphologically normal subjects. Clin Biomech 2014; 29: 444–450.
Schwarzkopf R, Dong NNG, Fetto JF: Finite element analysis of femoral neck stress in relation to pelvic width. Bull NYU Hosp Jt Dis 2011; 69: 292–297.
Spahn G, Kaiser M, Gantz S, Schiltenwolf M, Hartmann B, Schiele R, Hofmann G: Systematisches Literatur-Review und Metaanalyse zur Bestimmung von Risiko-faktoren für die Koxarthrose. ASU Arbeitsmed Sozialmed Umweltmed 2014; 49: 207–222.
Stelzner G: Zur Modellierung und Simulation biomechanischer Mehrkörpersysteme. Karlsruhe: Universitätsverlag Karlsruhe, 2009.
Stops A, Wilcox R, Jin Z: Computational modelling of the natural hip: a review of finite element and multibody simulations. Comput Methods Biomech Biomed Engin 2012; 15: 963–979.
Sulsky SI, Carlton L, Bochmann F, Ellegast R, Glitsch U, Hartmann B, Pallapies D, Seidel D, Sun Y: Epidemiological evidence for work load as a risk factor for osteoarthritis of the hip: a systematic review. PLoS One 2012; 7: e31521.
Taddei F, Martelli S, Valente G, Leardini A, Benedetti MG, Manfrini M, Viceconti M: Femoral loads during gait in a patient with massive skeletal reconstruction. Clin Biomech 2012; 27: 273–280.
Truszczyska A, Rpaa K, Gmitrzykowska E, Trzaskoma Z, Drza-Grabiec J: Postural stability disorders in patients with osteoarthritis of the hip. Acta Bioeng Biomech / Wrocaw Univ Technol 2014; 16: 45–50.
Valente G, Taddei F, Jonkers I: Influence of weak hip abductor muscles on joint contact forces during normal walking: probabilistic modeling analysis. J Biomech 2013; 46: 2186–2193.
Van der Krogt MM, Delp SL, Schwartz MH: How robust is human gait to muscle weakness? Gait Posture 2012; 36: 113–119.
Weißgraeber P, v d Wall H, Khabbazeh S, Kroker AM, Becker W: Effect of the lateral rotators on load transfer in the human hip joint revealed by mechanical analysis. Ann Anat 2012; 194: 461–466
Interessenkonflikt: Für beide Autoren besteht kein Interessenkonflikt.
Für die Verfasser
Dipl.-Ing. Patrick A. Varady
Berufsgenossenschaftliche Unfallklinik Murnau
Prof.-Küntscher-Straße 8
82418 Murnau
Fußnoten
1 Institut für Biomechanik, Berufsgenossenschaftliche Unfallklinik Murnau, Deutschland
2 Institut für Biomechanik Paracelsus Medizinische Privatuniversität Salzburg, Österreich